推荐图文

推荐新闻

点击排行

地基土水平抗力系数的比例系数m与其弹性模量E关系的数值试验研究

2015-12-08 6210 0

核心提示：周昌林，朱爱军(贵州大学，贵州贵阳 550025)　　摘要：在桩基设计中，地基土水平抗力系数之比例系数m是一个极为重要的参数。目

周昌林，朱爱军
(贵州大学，贵州贵阳 550025)

　　摘要：在桩基设计中，地基土水平抗力系数之比例系数m是一个极为重要的参数。目前在工程中，对系数m的取值主要借助于经验公式、查规范表和单桩水平静载试验。本文提出一种新的方法—数值试验法，在一模型中运用该方法成功地求出已知地基土弹性模量E下的水平抗力系数之比例系数m。基于该模型，我们进行单因素数值试验来探究地基土水平抗力系数之比例系数m与其弹性模量E之间关系。通过对试验数据进行回归分析得出在单因素数值试验中，地基土水平抗力系数m与其弹性模量E呈线性正相关的联系。最后，提出正交试验来从整体上研究桩刚度、地质条件等因素对地基土水平抗力系数之比例系数m的影响程度。
　　关键词：地基土水平抗力系数之比例系数；弹性模量；数值试验；回归分析
　　0 引言
　　桩基础是应用广泛的一种基础类型^[1]，除了承受竖向荷载还往往受水平荷载的作用。鉴于横向受荷桩承载力的重要性，我国建筑、路桥、铁道等部门的有关规范中对横向受荷桩的计算与设计要求均有不同程度的反映。由于地基土横向抗力系数的选取直接影响着横向荷载下桩基的位移和内力计算结果，因此如何选择并确定该系数，使之既安全可靠又合理适用是非常重要的^[2]。
　　在桩基设计中地基土水平抗力系数之比例系数m是一个较为关键的参数，目前工程中对参数m的取值主要由经验公式、查规范表和单桩水平静载试验来确定^[3-4]。在工程实际运用中却发现：经验公式所需参数单桩水平临界荷载H_cr、单桩水平临界荷载对应的位移x_cr均需做单桩水平静载试验并对试验数据进行一定的处理后方可得到。由于载荷试验费用高，在一般工程设计中，多数利用规范查表确定m值的方法^[5]。确定m值的规范法，由于每类土的m值上下限相差很大，如果没有其他土质性能指标可供参考，势必在运用时造成很大的任意性，从而影响计算结果^[6]。同时，根据地质勘查报告等资料，我们易获取土体变形模量、泊松比、内摩擦角、粘聚力、密度等参数，可据此反算出参数m。
　　基于上述问题，本文提出利用“m”法及大型通用有限元分析软件ANSYS做数值试验的方法来确定地基土水平抗力系数的比例系数m值。
　　1 m法简介
　　在线弹性地基抗力法中，地基抗力系数C如何随深度z变化，国内外学者对此有多观点，比较适用的一种^[2]： m法——假定地基系数C随深度呈正比例增加，即C=mz，如图1所示。

图1 地基土水平抗力系数分布图式

　　“m”法的基本前提是Winkel假定，即线弹性地基抗力法，它是用一组独立的离散型弹簧代替支挡结构开挖侧土体对支挡结构的抗力作用。该法克服了张氏法k为常数的缺点，能较好地反映地基系数沿深度分布的情况。此时桩的微分方程式为：

　　m法是迄今为止世界上运用最为广泛的计算方法，在英国、美国、前苏联、中国都把该方法列入规范之中，其比例系数m值可通过侧向荷载试验直接获得。
　　m法仅能反映土的弹性性能，在桩身位移较小时，能很好地反映桩土相互作用。当水平荷载较大且桩在泥面处发生较大位移时，桩侧土体进入塑性工作状态，用m法计算则出现较大误差，并且随着桩顶位移的增大，误差也随之较多的增大。m法在桩身位移较小的情况下比较适宜，而在实际工程中结构的位移均比较小，因此该方法也在建筑工程和公路桥涵的基桩基础设计中被广泛使用。
　　2 研究思路
　　根据《建筑桩基技术规范》^[3]第5.7.5条第2款，地基土水平抗力系数的比例系数m，宜通过单桩水平静载试验来确定，我们可用数值试验来模拟进行。基于ANSYS平台可计算出给定荷载下的桩顶水平位移，利用数值法和“m”法算出的桩顶水平位移相等，通过构造方程进行数值分析可反算出参数m。
　　3 数值实验分析
　　地基土水平抗力系数的比例系数m（MN/m⁴）（为地面以下2(d+1) m深度内各土层的综合值^[3]。通过ANSYS进行数值模拟求得桩顶水平位移，根据《建筑边坡工程技术规范》[7]查表可大致确定土体水平抗力系数的比例系数m的分布区间，借鉴《数值分析》二分法及迭代法^[8]原理，通过“m”法法来计算桩顶水平位移，直至所选土体水平抗力系数的比例系数m达到一定精度。
　　3.1 物理模型
　　选取钢筋混凝土圆截面桩作为研究对象，研究土体弹性模量E与其水平抗力系数的比例系数m的关系。
　　（1）几何模型：桩长23.5m，直径d=1.6m，桩的自由段长为1m，嵌岩段长3m，如图2所示。土体、基岩平面尺寸在桩周各外扩2倍桩长，桩底基岩向下延伸1倍桩长。

图2 桩基示意图（m）

　　（2）材料特性及参数
　　本模型是以贵州某一水平受荷嵌岩桩为工程背景，场地各岩土层自上而下为：红粘土，中风化石灰岩。桩为线弹性材料；土体(可塑)为E-µ模型,屈服准则是DP破坏准则；基岩为DP材料。通过查阅大量的工程地质资料及工程地质手册[9]，桩基各参数选取见表1。

表1 桩基采用的物理力学参数

参数	基桩	土体	基岩
弹性模量/GPa	26	0.010.05	12
泊松比	0.2	0.35	0.26
密度/(kg*m^-3)	2500	1740	2680
粘聚力/kPa	-	24.62	300
内摩擦角/^o	-	8.9	30
膨胀角/^o	-	8.9	28

　　（3）有限元模型
　　有限元计算采用大型通用有限元软件ANSYS,土体和基岩单元为SOLID45，桩单元为SOLID65。桩身本构关系采用线弹性，而土体本构采用非线性E-µ模型[10]。本算例采用的计算模型如图3所示，该模型的4个侧面及底部边界均被固定约束，在桩顶施加100kN的水平荷载。

图3 单桩模型及网格划分

　　3.2 确定地基土水平抗力系数的比例系数m
　　这里以E=19MPa时地基土水平抗力系数之比例系数m的确定为例来展示推导过程。在本模型中，我们基于ANSYS软件平台编辑APDL程序来计算，在ANSYS后处理进程中可查询出桩顶水平位移

。
　　基于此，我们构造出参数m的方程：

　　令

　　这里: m—土体水平抗力系数的比例系数(MN/m⁴);
　　

—“m”法计算得出的桩顶位移（mm）。
　　结合土体物理力学参数等信息，通过查阅《建筑边坡工程技术规范》表G.0.1-2 土质地基系数^[7]可初步确定土体水平抗力系数的比例系数

MN/m⁴。
　　由桩基传统解法可计算出

由此说明方程

在区间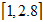

是有解的，我们选取的区间

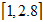是合理的。由二分法知：

　　据此，我们可取m=(1.98+1.99)/2=1.99为方程

的解。
　　3.3 两种解法的比较
　　通过ANSYS软件分析计算我们得出桩顶水平位移

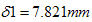，把m=1.99MN/m4代入理正结构设计工具箱软件求得桩顶水平位移

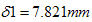，可见两种方式得出的桩顶水平位移基本吻合，说明这种研究方法是可行的。
　　4 土体弹模E与参数m的数值试验结果
　　在实践中，影响一个事物的因素往往是很多的，人们总是要通过试验，观察各种因素的影响，解决各因素对事物影响程度的有效方法之一就是方差分析^[11]。这里在方差分析的基础上，对试验结果进行回归分析。
　　实际上影响地基土水平抗力系数的比例系数m的因素很多，包括土质条件、水平荷载大小、桩刚度等因素^[12]。为了寻求土体弹性模量E与其水平抗力系数的比例系数m之间比较确切的函数关系，我们对该问题进行单因素数值试验，在这里我们仅改变土体弹性模量E的数值并按上述原理求解其对应的土体水平抗力系数系数的比例系数m,见表2。

表2 m与土体弹模E的对应关系

序号	弹性模量E(GPa)	桩顶水平位移δ(mm)	水平抗力系数的比例系数m(kN/m⁴)
1	0.019	7.82	1.99
2	0.022	7.22	2.44
3	0.025	6.72	2.95
4	0.028	6.35	3.43
5	0.031	6.04	3.93
6	0.034	5.76	4.47
7	0.037	5.51	5.05
8	0.04	5.31	5.62
9	0.043	5.11	6.24
10	0.046	4.94	6.88
11	0.049	4.79	7.52

　　这里我们采用最小二乘法^[8,11]来拟合m与E的函数关系，为方便我们求出拟合函数，我们首先需要作出m与E的散点图，见图4。

图4 弹模E与m的散点图

　　根据经验并结合该散点图可假设

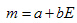,这里a和b均为待定系数。据此，我们把问题转化到线性回归^[12]问题上，即求一元线性回归方程。这里n=11,为求线性回归方程，对所需要的计算数据列于表3，

表3 回归方程的计算数据


1	0.019	1.99	0.000361	3.9601	0.03781
2	0.022	2.44	0.000484	5.9536	0.05368
3	0.025	2.95	0.000625	8.7025	0.07375
4	0.028	3.43	0.000784	11.7649	0.09604
5	0.031	3.93	0.000961	15.4449	0.12183
6	0.034	4.47	0.001156	19.9809	0.15198
7	0.037	5.05	0.001369	25.5025	0.18685
8	0.04	5.62	0.0016	31.5844	0.2248
9	0.043	6.24	0.001849	38.9376	0.26832
1	0.046	6.88	0.002116	47.3344	0.31648
11	0.049	7.52	0.002401	56.5504	0.36848
	0.374	50.52	0.013706	265.7162	1.90002

　　由此可得

　　所以得出回归直线方程：

，此函数关系说明在保持土质条件、桩刚度、水平荷载等因素相同的条件下，地基土水平抗力系数之比例系数m与其弹性模量E呈现出线性正相关的联系。该研究成果有助于我们对地基土水平抗力系数之比例系数m进行更精确的取值，同时发现《建筑边坡工程技术规范》（2013）对参数m的取值比《建筑桩基技术规范》（2008）的更精确。
　　5 结语
　　本文利用ANSYS、“m”法，借鉴二分法原理及迭代思想并通过数值试验来研究地基土水平抗力系数之比例系数m与其弹性模量E之间的关系。通过算例成功地计算出已知地基土弹性模量E下的水平抗力系数之比例系数m，并且通过“m”法进行计算得到的桩顶位移这一传统解与基于ANSYS软件平台得到的桩顶位移数值解基本上吻合，说明这种研究方法是可行的。
　　5.1 主要结论
　　在该算例的基础上利用这种数值法分析了不同弹性模量E对应下的地基土水平抗力系数之比例系数m，并对通过数值试验得到数据进行回归分析，得出以下结论：
　　(1) 数值试验法是一种不同于传统求解的新方法，为桩基研究提供一种较新的思路。
　　(2) 在进行单因素数值试验分析中，地基土水平抗力系数之比例系数m与其弹性模量E呈线性正相关的联系，并且在试验中发现弹模E对参数m比较敏感。
　　5.1 需要进一步研究的问题
　　影响地基土水平抗力系数之比例系数m的因素很多，本文只做了局部性的探究，若要从整体上研究各因素对m的影响程度，对各因素进行正交试验是一种比较新的方法。
　　参考文献：
　　[1] 王成.桩基计算理论及实例[M]. 成都：西南交通大学出版社，2011:2.（Wang Cheng. Calculating theory and practice of pile foundation[M]. Chengdu: Southwest Jiaotong University Press, 2011:2.（in Chinese））
　　[2] 经永新. 地基土横向抗力系数分析与适用于钢筋混凝土桩m值的确定[J].建筑结构学报, 1996, 17(3):73–78.（Jing Yong-xin. Analysis coefficients of lateral subgrade and determination of parameter m for precast RC piles[J]. Journal of Building Structures, 1996, 17(3):73-78.（in Chinese））
　　[3] 中华人民共和国住房和城乡建设部. 建筑桩基技术规范[S].北京：中国建筑工业出版社, 2008:63-64,127-128,295.（Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical code for building pile foundations[S]. Beijing: China Architecture & Building Press, 2008:63-64,127-128,295.（in Chinese））
　　[4] 中华人民共和国交通部. 公路桥涵地基与基础设计规范[S].北京：人民交通出版社, 2007:84-85.（Ministry of Transport of the People’s Republic of China. Code for Design of Ground base and Foundation of Highway Bridges and Culverts[S]. Beijing: China Communications Press, 2007:84-85.（in Chinese））
　　[5] 邢恩桥,许国辉,杨俊杰. 用静力触探参数确定地基土水平地基抗力系数的比例系数m值-以天津地区为例[J].中国海洋大学学报, 2005,35(4):683–686.（Xing En-qiao, Xu Guo-hui, Yang Jun-jie. Determination of the values of proportional coefficient paramete m of the horizontal resistance coefficient of foundation soils in terms of static CPT parameters: case studies in Tianjin[J]. Periodical of Ocean University of China, 2005, 35(4):683-686.（in Chinese））
　　[6] 熊巨华，李建华. 基坑围护工程中土体水平抗力系数m值的分析与确定[J].建筑结构学报, 1998, 6:39–41.（Xiong Ju-hua, Li Jian-hua. Analysis and determination of the coefficient of lateral resistance in project of supported pit[J]. Journal of Building Structures, 1998, 6:39-41.（in Chinese））
　　[7] 中华人民共和国建设部. 建筑边坡工程技术规范[S].北京：中国建筑工业出版社, 2013：121.（Ministry of Development of the People’s Republic of China. Technical code for building slope engineering[S]. Beijing: China Architecture & Building Press, 2013:121.（in Chinese））
　　[8] 张民选，罗贤兵.数值分析[M]. 南京：南京大学出版社，2013:12-15,84-88.（Zhang Min-xuan, Luo Xian-bing. Numerical analysis[M]. Nanjing: Nanjing University Press, 2013: 12-15, 84-88.（in Chinese））
　　[9] 《工程地质手册》编委会.工程地质手册（第四版）[M]. 北京：中国建筑工业出版社, 2007:160-161,446.（Writing Committee of Engineering Geology Manual. Engineering Geology Manual(the 4th editon)[M]. Beijing: China Architecture & Building Press, 2007:160-161,446.（in Chinese））
　　[10] 王伟. ANSYS14.0土木工程有限元分析从入门到精通[M]. 北京：清华大学出版社，2013:324（ Wang Wei. From the Entry to the Master of Finite Element Analysis in Civil Engineering[M]. Beijing: Tsinghua University Press, 2013: 324.（in Chinese））
　　[11] 陈魁. 应用概率统计[M]. 北京：清华大学出版社，2000: 218, 240-243.（ Chen Kui. Applied probability and statistics [M]. BEIjing: Tsinghua University Press, 2000: 218, 240-243.（in Chinese））
　　[12] 马志涛. 水平荷载下桩基受力特性研究综述[J].河海大学学报（自然科学版）, 2006, 34(5):546-551.（Ma Zhi-tao. Study on behavior of pile foundation under lateral loading[J]. Journal of Hohai University (Natural Sciences), 2006, 34(5):546-551.（in Chinese））

（本文来源：第十二届全国桩基工程学术会议论文集）

上一篇：钻孔压灌桩成桩新工艺

下一篇：海卓帕斯电子水处理器的优势

点赞（0）
反对（0）
举报（0）
收藏（0）
分享（19）

评论(0)

同类新闻更多 >>