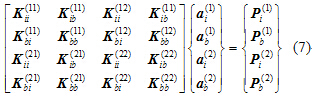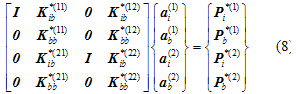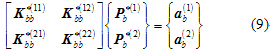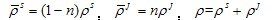
式中 、
、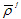 和
和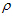 分别为固相、液相和混合体的总体密度,
分别为固相、液相和混合体的总体密度,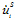 为固相速度,
为固相速度,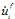 为液相速度,
为液相速度,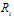 为固液相相互作用力,
为固液相相互作用力,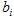 为单位质量体积力。饱和土中有效应力与总应力的关系为:
为单位质量体积力。饱和土中有效应力与总应力的关系为:
其中:

将式(2)、式(3)代入式(1),再根据上述三个假定可得:
式中
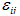
、
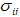
为应变张量和应力张量,
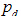
为孔压中的动力分量,
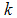
为渗透系数,
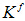
为土中液相刚度,
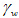
为水重度,其余符号含义如前所示。
2.2 方程空间离散
对方程(4)进行空间离散,可得
式中
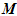
,
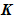
,

,
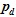
,
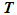
和

分别为质量矩阵,刚度矩阵,液相刚度矩阵,动孔压矩阵,表面力矩阵和固相位移矩阵;
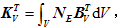
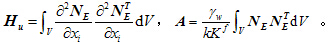
采用时域内无条件稳定的Newmark方法进行空间离散,令
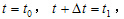
最终可得:
式中:
2.3 边界条件
为解决动力有限元问题,需要设置合适的边界条件,为减少系统的总自由度,本文采用子结构法对模型进行凝聚处理。子结构与其他子结构或单元连接前,在该层子结构内将内部自由度凝聚掉,凝聚前与凝聚后的子结构节点如图1所示。
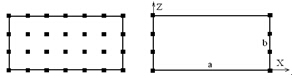 (a) 凝聚前子结构 (b)凝聚后子结构
(a) 凝聚前子结构 (b)凝聚后子结构
图1 凝聚前与后的子结构节点
Fig. 1 Nodes of the pre-condensed and post-condensed sub-structure
子结构内按最小半带宽的要求进行节点编号,这时结构的内部节点和交界面的节点方程为式(7),其中
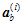
为交界面节点自由度,
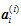
为需要被凝聚的自由度。通过Gauss-Jordan消去法可得式(8)。
化简式(8)可得式(9):
3 算例验证
本文以Lamb问题为算例,验证所采用计算方法与人工边界条件的正确性。其解析解已由Lamb给出[18]。计算参数取自文献[18],计算结果如图2。由图可知,采用本文所述的计算方法所得的数值结果与解析解答吻合较好,由此可见本文方法的正确性。对比有、无人工边界条件计算结果,可见本文的人工边界可以较好地透射出外行波,是一种有效的人工边界条件。
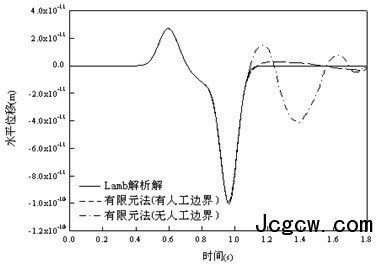 图2 Lamb问题计算结果对比图
图2 Lamb问题计算结果对比图
Fig. 2 Computational results comparison of Lamb’s problem
4 计算结果分析
文献[17]表明群桩能够起到明显的减振作用,并增加桩-土体系刚度和质量,减小承台位移;在分层地基中上硬下软地基比上软下硬地基减振效果好。为进一步分析群桩在列车竖向动荷载作用下地表测点的振动,以饱和的多孔介质地基为基础,分别计算了不同桩型、桩长、渗透系数、土体泊松比以及桩身弹性模量下群桩模型地面动力响应。
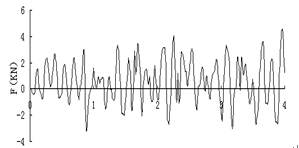 (a) 激振点动荷载时程曲线
(a) 激振点动荷载时程曲线
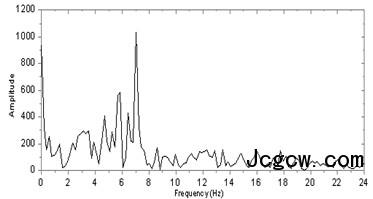
(b) 激振点动荷载频谱曲线
图3 激振点动荷载曲线
Fig. 3 Dynamic loading curves at the excitation point

(a) 4根群桩布置图
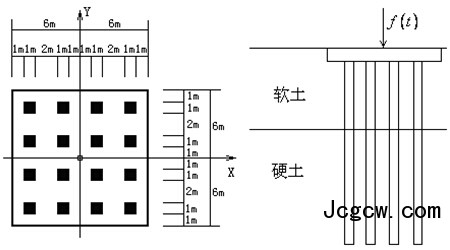
(b) 16根群桩布置图
图4不同群桩布置图
Fig. 4 Different layouts of pile groups 图3为作用于承台中心的竖向动荷载时程和频谱曲线,图4为4根和16根两种群桩布置图,表1和表2为土层和桩身的计算参数,其中E为弹性模量,k为渗透系数,n为孔隙率。在下文分析中,采取控制变量法进行分析。以4根群桩、上软下硬土层为例,分析参数变化对计算结果的影响。
4.1不同布桩对隔振效果的影响
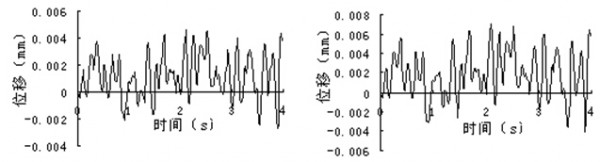
图5、图6为16根和4根群桩模型分别在原点和距原点8m处的竖向位移峰值曲线,由图可知在上软下硬土层中大型群桩模型能够明显的减小地表和承台表面各测点的竖向位移峰值。图7表明大型群桩基础在一定程度上能有效地减小竖向位移幅值,并且对群桩周围土体影响较大。但采用何种布桩型式控制地表振动应综合考虑工程造价和设计要求。
(a) 16根桩位移时程曲线 (b) 4根桩位移时程曲线
图5原点处位移时程曲线
Fig. 5 The displacement time history curve at point of origin
4.2群桩桩长对隔振效果的影响
为分析群桩桩长的动力响应影响,分别取桩长为6m和10m计算。图8至图10为4根群桩不同计算点位的位移时程和幅值曲线。由图可知,增加桩长可在一定程度上减小上软下硬地层地表土体和承台表面的竖向位移幅值。即增加桩长是保证短桩隔振效果的可行方法,但这种方法不能够大幅度的减小竖向位移幅值,且在实际工程中还应考虑增加桩长而引起的增加工程造价和施工难度等。
4.3土层渗透系数k的影响
图11-图13为4根群桩上层软土渗透系数k取不同数值时测点的位移时程和幅值曲线。由图可知,即使渗透系数不同,地表各测点的位移峰值曲线的变化趋势也是相似的。综合不同桩型及不同土层的计算模型可得,土体渗透系数的增大虽然对模型的减振效果有利,但承台周围土体体积较大,对承台表面各个测点位移幅值的影响较小。
4.4土体泊松比 的影响
图14-图16为4根群桩地基土泊松比 取不同数值时测点的位移时程和幅值曲线。
由图14、图15可知,随着土层泊松比取值的增加模型的隔振效果趋于明显,尤其在承台以外地表测点部分。不同测点处竖向位移峰值随土体泊松比增加而变化的曲线如图16所示,即随测点距原点距离的增加,泊松比对隔振效果的影响越小。
4.5混凝土弹性模量E的影响
图17至图19为4根群桩的混凝土性模量E取不同数值时测点的位移时程和幅值曲线。
由图17和图18可知,随着混凝土弹性模量取值的增大,竖向动荷载作用点附近的位移幅值有较明显的减小;但随着测点与原点距离的增加,土体表面的位移幅值差异逐渐减小,最终趋于一致。
由图19可知,如果桩身和承台的模量取值较高,可有效地减小动荷载作用点附近的竖向位移。但随测点与作用点距离的增加,两者的差异同样的趋于一致。故如果在上软下硬的地基土中设置群桩,提高桩基弹性模量可有效减小作用点处振动位移,但不能减小较远处地表的振动幅值。
5 结 论
利用三维饱和介质中有限元的计算模型,计算了不同地质条件下不同布桩的群桩动力响应,分析了模型的物理力学参数及几何参数对群桩动力响应的影响,得出结论如下:
(1)不同布桩对竖向振动的隔振效果是不同的,16根大型密布群桩的隔振效果明显的优于4根小型桩基,其差异取决于土层条件和桩身的材料参数。
(2)增加桩长可在一定程度上提高群桩基础的刚度,减小基础的竖向位移,但幅值减小与桩长的增加量在工程设计中应综合分析。
(3)土层渗透系数的变化对承台上各测点的位移幅值影响较小。但随着渗透系数的增加,与原点距离较远的地表测点的位移幅值略有减少,这对周围土体隔振有一定效果。
(4)土体的泊松比对群桩的振幅影响非常明显,尤其是距原点较远的地表土层测点。如土层泊松比取大值时,其位移幅值可减小约50﹪。
(5)桩身材料取弹性模量大的高强混凝土,可有效减少承台顶面的位移幅值,但对较远处地表的振动影响较小。
参考文献
[1] TAJIMI H. Dynamic Analysis of a structure embedded in an Elastic Stratum[C]//Proceedings of 4th World Conference on Earthquake Engineering. Santiago: [s. n.], 1992: 53-59.
[2] NOVAK M, ABOUL E F. Dynamic stiffness and damping of piles[J]. Canadian Geotechnical Journal, 1974, 11(4): 574- 598.
[3] NOVAK M, ABOUL E F. Impendence Functions of pile in layered media[J]. Journal of Engineering Mechanics, ASCE, 1978, 104(6): 643-669.
[4] ZENG X, RAJAPAKSE R K N D. Dynamic axial load transfer from elastic bar to poroelastic medium[J].Journal of Engineering Mechanics, 1999, 125(9): 1 048-1 055.
[5] WANG J H, ZHOU X L, LU J F. Dynamic response of pile groups embedded in a poroelastic medium[J]. 2003,23(3): 235-242.
[6] 周香莲,周光明,王建华. 水平简谐荷载作用下饱和土中群桩的动力反应[J]. 岩石力学与工程学报,2005,24 (8): 1433-1438 (ZHOU Xiang-lian, ZHOU Guang-ming,WANG Jian-hua. Dynamic response of pile group in saturated soil subjected to horizontal loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24 (8): 1433-1438)
[7] DOBRY R, GAZETAS G. Simple method for dynamic stiffness and damping of floating pile groups [J]. Geotechnique, 1988, 38(4): 557-574.
[8] MAKINS N, GAZETAS G. Dynamic pile-soil-pile interaction. Part II: Lateral and seismic response [J]. Earthquake Engineering & Structural Dynamics. 1992, 21(2): 145–162,
[9] MYLonAKIS G, GAZETAS G. Lateral vibration and internal forces of grouped piles in layered soil [J] Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(1): 16-25
[10] 高广运,赵元一,高盟,杨成斌. 分层土中群桩水平动力阻抗的改进计算[J]. 岩土力学,2010, 31(2): 509-515 (GAO Guang-yun, ZHAO Yuan-yi, GAO Meng, YANG Cheng-bin [J]. Rock and Soil Mechanics, 2010, 31(2): 509-515 (in Chinese))
[11] 燕彬,黄义. 柔性承台板与群桩的竖向动力作用[J]. 地震工程与工程振动,2004,24(5): 136-140. (YAN Bin, HUANG Yi. Dynamic interaction of axial vibration between pile groups and flexible plates [J]. Earthquake Engineering and Engineering Vibration, 2004,24(5): 136-140 (in Chinese))
[12] WOLF J P, VonARX G A. Impedance function of a group of vertical piles [C]. Proceedings of the ASCE Geotechnical Engineering Division Specialty Conference, June 19-21, 1978, Pasadena, California. ASCE, Volume I of Earthquake Engineering and Soil Dynamics: 1024-1041
[13] PADRON L A, AZNAREZ J J, MAESO O. BEM–FEM coupling model for the dynamic analysis of piles and pile groups [J]. Engineering Analysis with Boundary Elements, 2007, 31(6): 473-484
[14] ZHANGH H, SMALL J C. Analysis of capped ré$e gou0ó subected tOТocIzot`m†a vmtica| 聬oas聛.`Kmtutrs and耠Geo聴chcr,02蠰0倬 :Ш):1-2耍尚守帳,于俊. 栩渎坟非线愧耦琈扭赨戯动特戧分 [J].伭噽兼路技,2009. 22(5): 41-47. (SHANG耠Shou- ping, YU Jun. Analysis of Dynamic Behaviors of Pile-soil Ngnlinear Coupling Torsional Vibration [].China Joural of Highway and Transto2t,2009. 22(5): 41-47)
[16] ZIENKIE×ICZ O C, PAUL D K CHAN A`H C. Unconditionallq stable staggere$ solution procedure forsoil-pore flui聤 interaction probems [J]. Int. J Number Anal Methds Geotechnical Engineering, 1988, 26(5): 1039 -55
[17] 高广运,王非,赵宏,赵元一. 分层地基中群桩的动力响应及减振分析[J]. 岩土工程学报,2013,S2:1108-1112(GAO Guang-yun, WANG Fei, ZHAO Hong, ZHAO Yuan-yi. Analysis on dynamic response and ground vibration isolation by group pile in layered ground[J]. Chinese Journal of Geotechnical Engineering, 2013, S2: 1108-1112)
[18] LAMB H. On the propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society of London, Series A, 1904, (203):1-42

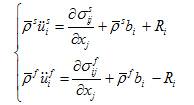
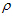 分别为固相、液相和混合体的总体密度,
分别为固相、液相和混合体的总体密度,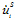 为固相速度,
为固相速度,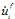 为液相速度,
为液相速度,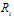 为固液相相互作用力,
为固液相相互作用力,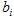 为单位质量体积力。饱和土中有效应力与总应力的关系为:
为单位质量体积力。饱和土中有效应力与总应力的关系为:
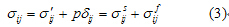
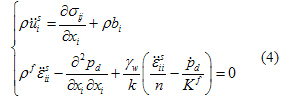
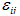 、
、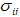 为应变张量和应力张量,
为应变张量和应力张量,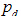 为孔压中的动力分量,
为孔压中的动力分量,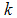 为渗透系数,
为渗透系数,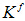 为土中液相刚度,
为土中液相刚度,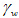 为水重度,其余符号含义如前所示。
为水重度,其余符号含义如前所示。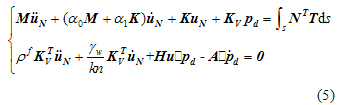
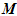 ,
,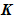 ,
, ,
,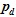 ,
,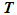 和
和 分别为质量矩阵,刚度矩阵,液相刚度矩阵,动孔压矩阵,表面力矩阵和固相位移矩阵;
分别为质量矩阵,刚度矩阵,液相刚度矩阵,动孔压矩阵,表面力矩阵和固相位移矩阵;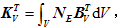
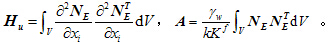
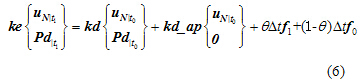
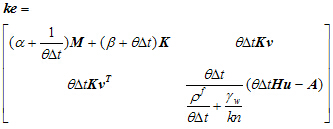

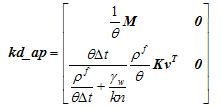

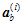 为交界面节点自由度,
为交界面节点自由度,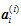 为需要被凝聚的自由度。通过Gauss-Jordan消去法可得式(8)。
为需要被凝聚的自由度。通过Gauss-Jordan消去法可得式(8)。