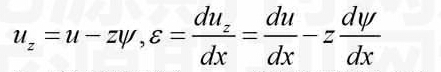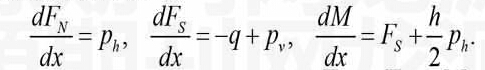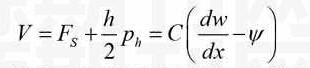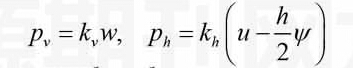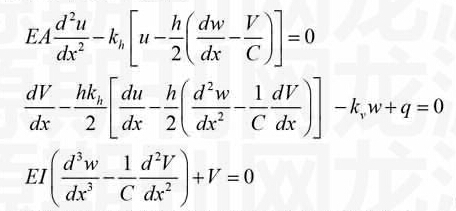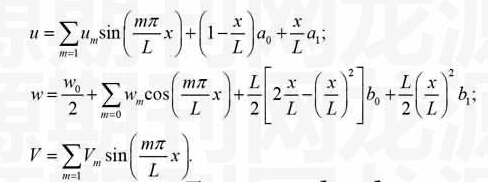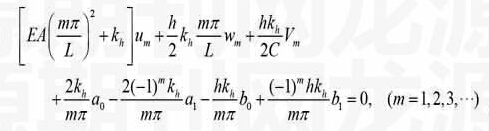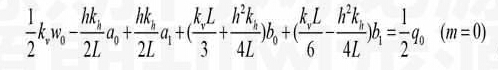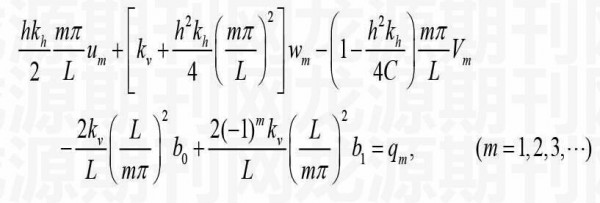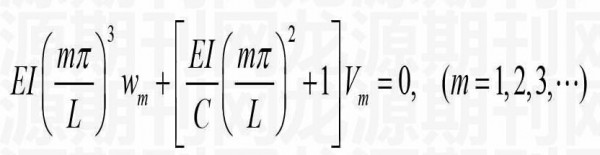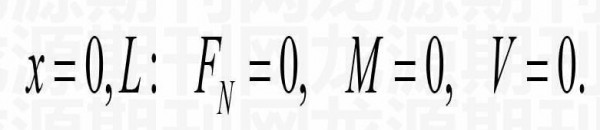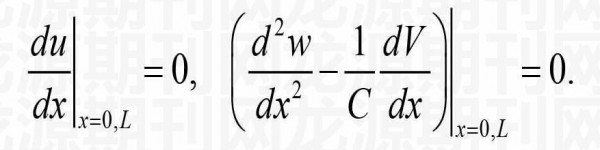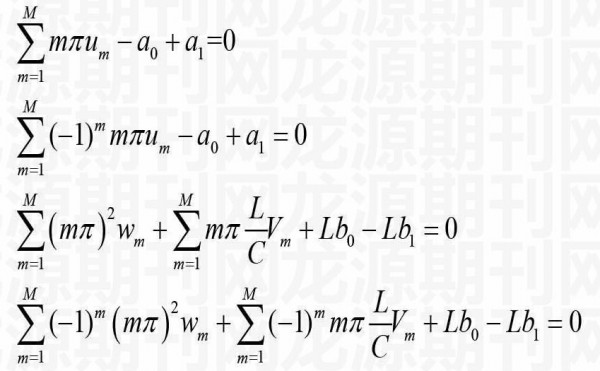考虑纵向摩阻时弹性地基上Timoshko梁弯曲的Fourier级数解答
2015-07-07
247
0
核心提示:考虑地基纵向摩擦力的影响,建立了广义Winkler型地基梁的平衡方程。假定纵向摩擦力与梁底面的纵向位移成正比,引入广义剪力,得到梁的位移型平衡方程。将位移及荷载展开为带附加项的Fourier级数,利用平衡方程和边界条件对弹性地基梁的一般弯曲进行分析。分析表明,纵向摩擦力对梁的位移和内力均有影响,其影响程度随着纵向反力系数和梁截面高度的增大而增大;梁的最大挠度、转角、弯矩及剪力随着地基纵向反力系数的增大而减小;梁的轴向位移和轴力则随着地基纵向反力系数的增大而增大。
1.引言
弹性地基梁是土木工程结构的基本构件,准确合理地对其进行计算具有重要的意义。传统分析方法中通常把地基抽象为Winkler模型、弹性半空间模型、双参数模型,梁则认为是Berlouli-Euler梁,假定梁与地基的接触面是光滑的,通过综合考虑梁、地基及两者之间的法向协调变形关系进行弹性地基梁的分析[1-3]。事实上,许多情况下还应该考虑剪切变形的影响[4];另外,梁与地基之间就客观上存在着摩擦力,这是因为梁与地基之间的接触面较为粗糙,混凝土材料与土的变形模量差异较大,使得梁-地基接触面的性质非常复杂所致。这种底面摩阻效应通常不容忽略,特别是梁的截面高度较大时,否则可能会造成较大误差。
国内外的一些学者通过分别假定摩擦力与梁的底面位移成正比,或与接触压力成正比,或假设梁底地基纵向力为线性分布,或假定纵向摩阻力为定值,分别通过直接求解特征方程、分步计算、伽辽金法、幂级数、微分算子级数法及有限元对计及纵向摩擦力的Bernoulli-Euler梁或Timoshenko梁进行了分析[5-13],得到了一些有益的结果。本文通过引入一个广义剪力,得到了以轴向位移、挠度和广义剪力为基本变量的梁的平衡方程,利用Fourier级数研究了考虑纵向摩擦力时Winkler型弹性地基上Tiomoshenko梁的一般弯曲。
2.Timoshenko梁的Fourier级数解答
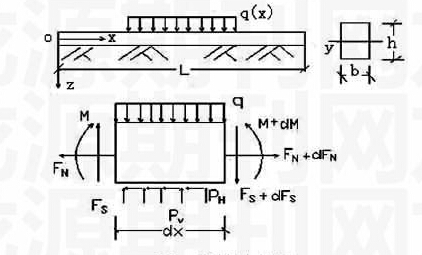
图1弹性地基梁
Fig.1abeamonelasticfoundation
设、依次为Timoshenko梁轴线处的轴向位移和截面转角,则梁截面上任一点的纵向位移和轴向应变为
(1)
让轴通过截面形心,、轴为截面的形心主轴,于是
(2)
上式中,为梁所用材料的弹性模量,为梁的横截面面积,为梁截面对中性轴的惯性矩。
对图1所示的弹性地基梁,不计轴向力产生的附加横向荷载,由所取梁段的平衡,得
(3)
式中,为梁所受到的横向荷载,、、依次为梁的轴力、剪力及弯矩,和地基对梁产生的纵向摩阻及横向反力。
参考文献[14]的处理方法,定义如下的广义剪力
(4)
这里,梁的剪切刚度,为截面修正系数。并假定地基为广义Winkler地基,即法向反力与梁的挠度成正比,切向反力与梁底面的纵向位移成正比,于是
(5)
其中,、、分别为地基法向反力系数、切向反力系数和梁的挠度。由式(2-5)可得到以位移、和剪力表示的梁的平衡方程如下
(6)
将作用在梁上的横向荷载展开为如下形式的Fourier级数
(7)
对两端自由梁,将梁的位移和剪力展开为如下形式的带附加项的Fourier级数[15]
(8)
其中的、及、、、为待定常数,级数中所加的附加项是为了保证和能连续进行必要次数的求导。
将式(7)、(8)代入式(6)中,再把、、、的系数展开为相应的Fourier正弦级数或余弦级数,通过系数比较得
(9)
(10)
(11)
(12)
两端自由弹性地基梁的边界条件如下:
(13)
由式(8)知,式(13)中的第三个边界条件已满足。式(13)中的第一、第二个边界条件得可改写为
(14)
将式(8)代入式(14)后,得
(15)
式(9-12)和(15)即为本文得到的求解弹性地基梁代数方程组。若级数取到前项,则待定系数、、及、、、总共有个,由式(9-12)和(15)组成的代数方程组中也共有个代数方程,因此问题可解。由式(9-12)和(15)求出系数、、及、、、后,代入式(8),可得到位移、及广义剪力(剪力接着由式(4)、(5)求出),再由式(4)、(2)可得到转角、轴力及弯矩。
3.算例及分析
设梁的长度,截面尺寸,截面修正系数,弹性模量,剪切模量,地基反力系数,,,,梁上所作用的荷载为均布荷载及集中力。计算结果见图2-7。
4.结论
(1)Fourier级数法是求解弹性地基梁的有效方法。
(2)当存在切向摩擦力时,梁的剪力不再与挠度的3阶导数成正比。
(3)切向摩擦力对梁的影响随着切向反力系数和梁截面高度的增大而增大。
(4)切向摩擦力的分布规律较为复杂,究竟哪一种规律与实际相符需要进一步的实验验证。