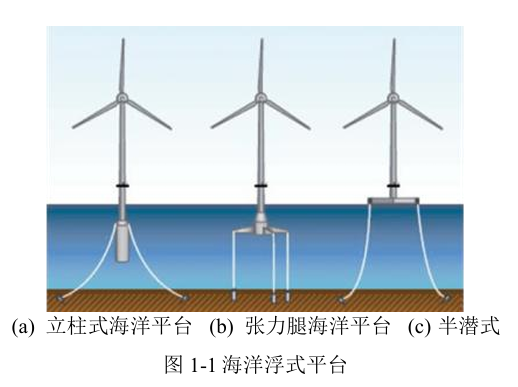

吸力桶形基础是一种大直径薄壁圆筒结构,底端敞口,上端为有抽气孔的封闭端,如图1-2(a)。
地基极限反力法(极限平衡法)
地基极限反力法假设土体各深度均处于极限状态,依据经验假定地基反力分布形式,认为地基反力p仅是深度z的函数与桩身位移y无关。水平承载力由作用在桩体上的力构成的平衡条件推导得出。地基极限反力法根据所假定的土抗力分布形式的不同,分为三种不同类型:
(1)土反力按二次抛物线分布,例如恩格尔(Engel)-物部法,是以前沉井和沉箱计算中常采用的方法;
(2)土反力按直线分布,例如冈部法、雷斯(Raes)法、斯奈特科(Snitko)法和布罗姆斯(Broms)法;
(3)土反力任意分布的方法,如挠度曲线法。上述几种方法的地基反力分布形式和被动土压力(系数)的分布情况如表1-1所示

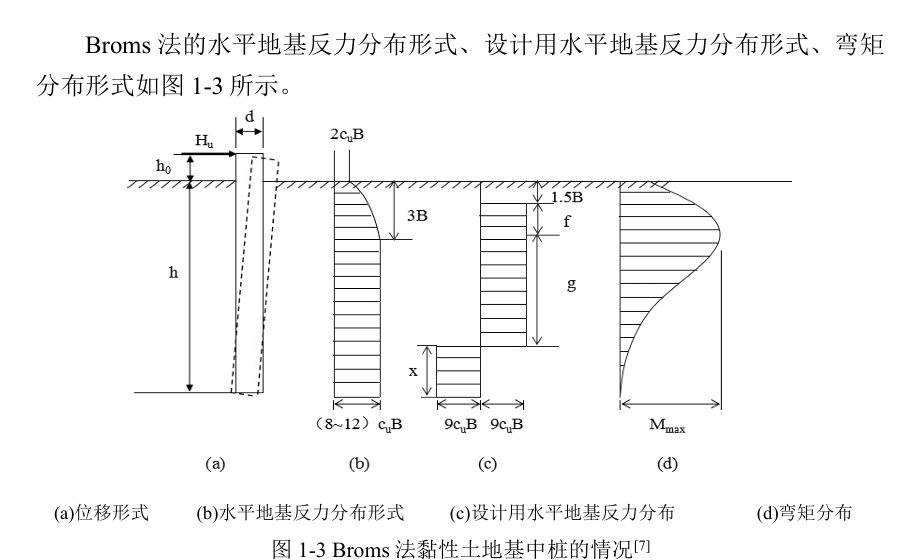
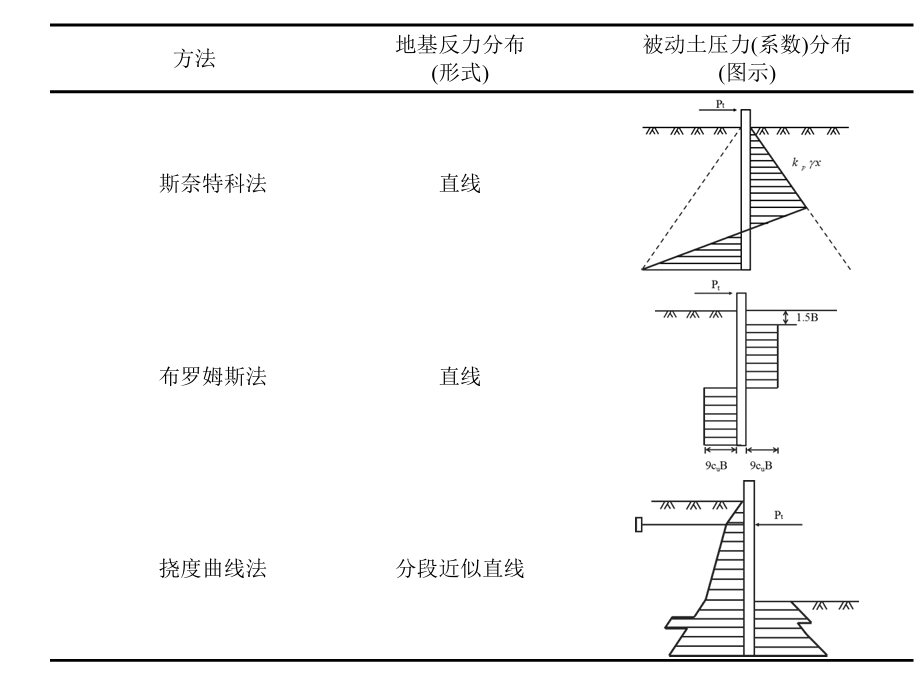
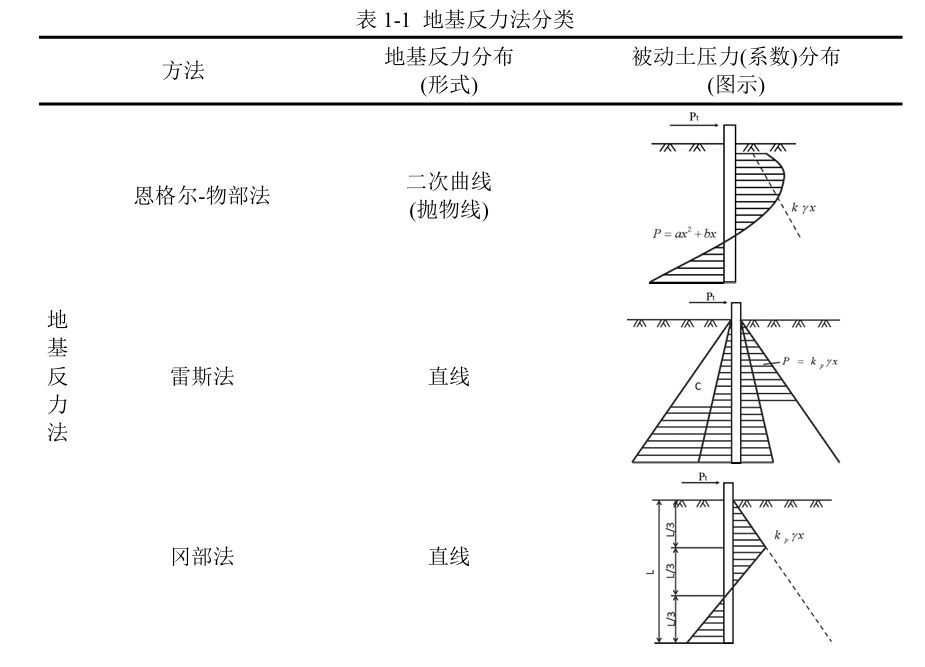
地基极限反力法优点是该法形式较为简单,但是认为桩侧反力与该处水平位移无关,桩侧反力处处达到极限状态,地基反力仅为深度的函数,且桩侧反力分布形式的假设情况与实际情况并不一致。为了将地基反力和桩身水平位移联系起来,提出了弹性地基反力法。
弹性地基反力法(弹性地基梁法)
(1)线弹性地基反力法

若弹性地基反力法按y的指数n来分类,通常分为n=1时的线弹性地基反力法和n≠1时的非线弹性地基反力法。目前一般规定水平荷载作用下单桩允许水平位移约为6~10mm,当水平位移在允许位移范围内时,桩侧土抗力和桩身水平位移可以近似认为呈线性增加。小位移使用线弹性地基反力法,反之则使用非线弹性地基反力法。
线弹性地基反力法采用Winkler假定,认为桩周土体是线弹性体,可以用用离散的一系列弹簧模拟桩土间的相互作用。采用弹性地基反力法求解水平荷载作用下的地基反力时,根据地基反力分布形式和水平地基反力系数k的不同,弹性地基反力法可分为常数法(也称张氏法)、k法、c法、m法以及综合刚度原理和双参数法等。
张氏法认为水平地基反力系数为常数,水平地基反力系数不随深度改变,故也称常数法。常数法在超固结黏土和密实砂土的均质地基中适用性很好。但应用在多层地基的计算时,其水平反力系数需要通过不断试算求得。因为该法计算过程比较复杂,不易推广使用,应用受限制。k法认为浅层的地基反力系数的形式由上至下按凹曲线变化,深层的地基反力系数保持不变。但有研究表明,由于k法假定近地面处的地基反力系数按凹曲线变化,导致计算的桩身弯矩偏大,计算的地基反力偏小。

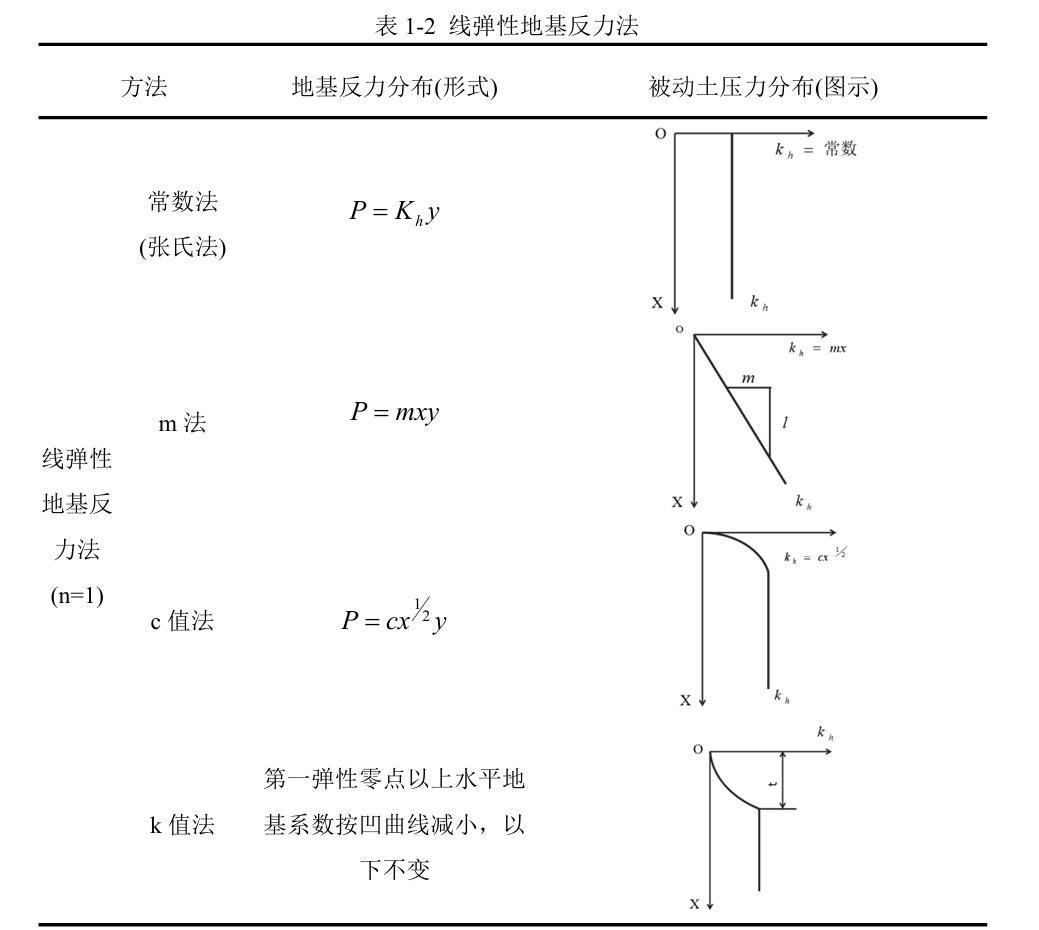
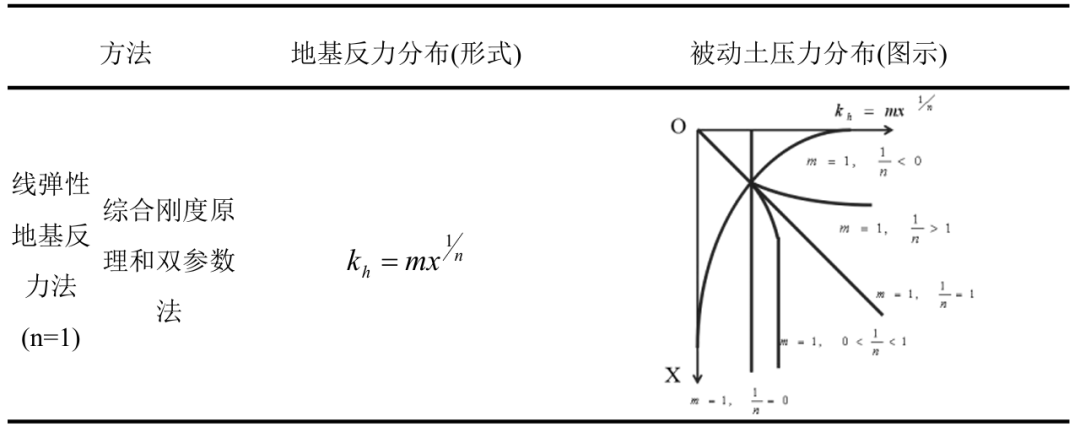
(2)非线性弹性地基反力法
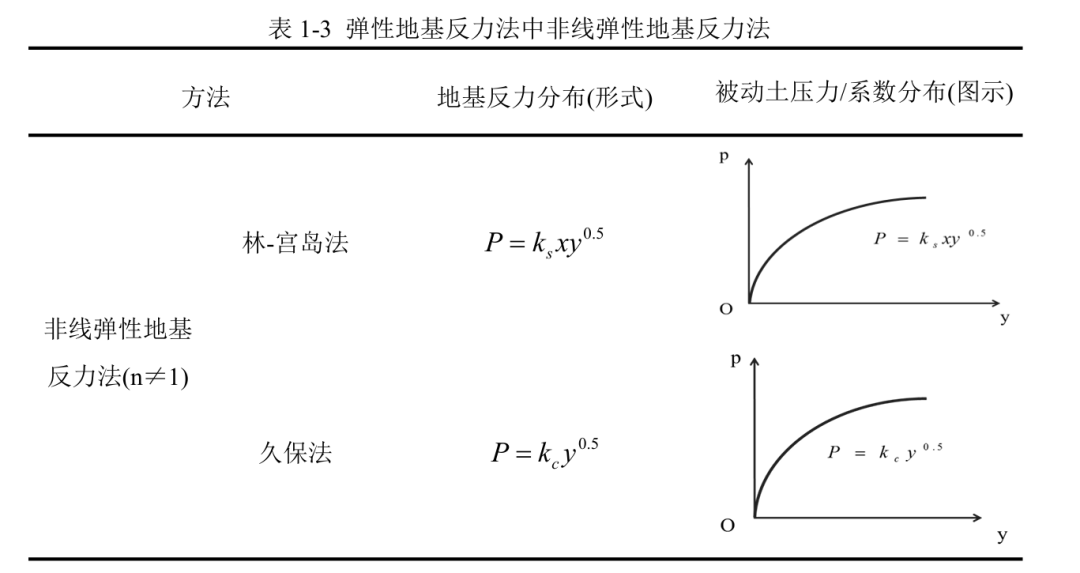
当桩受到较大水平力时,桩身侧移较大,桩侧土的变形和位移的关系不再是线性关系,学者们采用非线弹性模型来表达地基的非线弹性,最有代表性的方法有林-宫岛法(1963)和久保法(1964)。林-宫岛法适用于C型地基,久保法适用于S型地基,很难根据非线性微分方程的求解,计算较为复杂。所以使用非线性弹性地基反力法时采用相似法则,用由标准桩得到的标准曲线计算实际桩的受力状态。因其需要标准桩的试桩资料并且计算复杂,限制了非线性弹性地基反力法在工程设计中的应用。
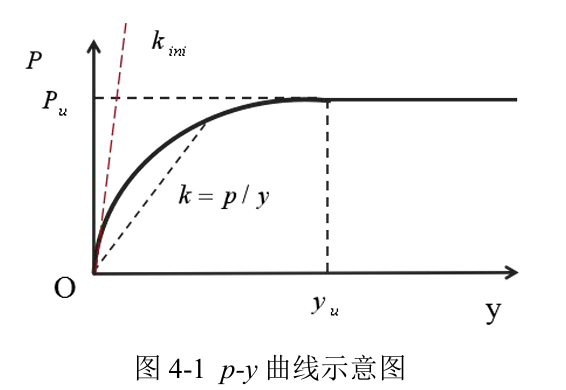
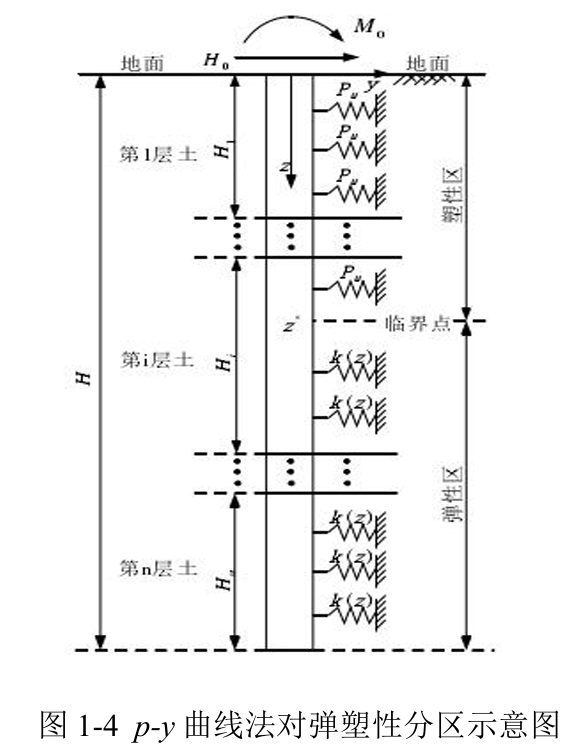
复合地基反力法是指在水平荷载作用下,泥面下某一深度研究点处的桩周土体水平地基反力与该点桩的挠度之间的关系曲线,是一种弹塑性分析方法。其中p表示研究点处桩周土体的水平地基抗力,y表示研究点处桩体的水平位移。在长桩桩顶受到水平力作用后,桩周土从地表面开始产生屈服塑性区并向下扩展。复合地基反力法在塑性区采用地基极限反力法,弹性区采用弹性地基反力法。根据弹性区和塑性区边界上的连续条件求桩的水平抗力。
根据对于弹性区和塑性区水平地基反力的不同假设,复合地基反力法分为长尚法、竹下法、斯奈特科法和p-y曲线法。
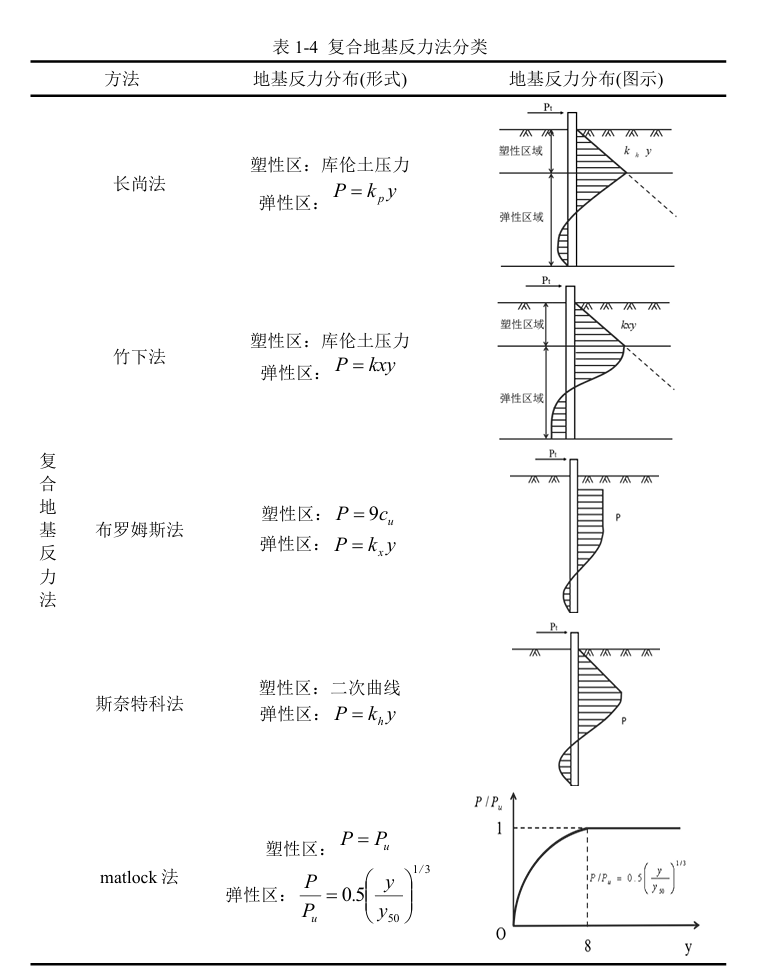
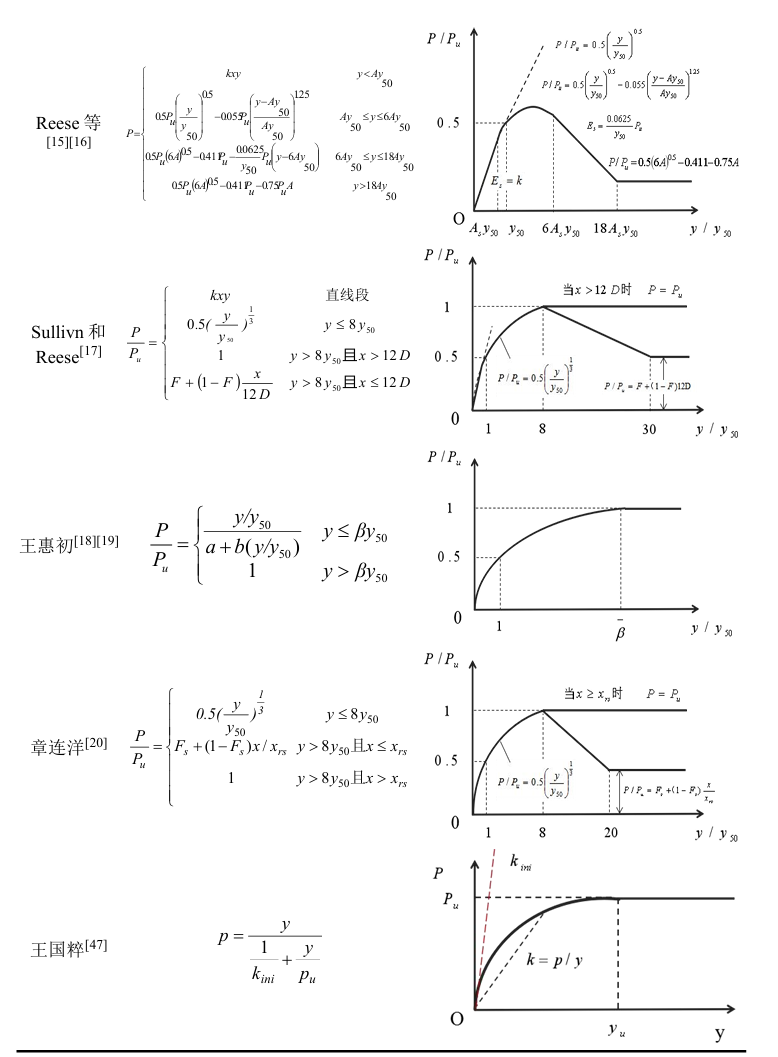
p-y曲线形式
不同学者给出了不同的p-y曲线模型,部分学者提出的p-y曲线主要公式及曲线形式如下表4-1所示。